The Energy And Pitfalls Of Mathematical Fashions: A Deep Dive

The Energy and Pitfalls of Mathematical Fashions: A Deep Dive

Associated Articles: The Energy and Pitfalls of Mathematical Fashions: A Deep Dive

Introduction

With nice pleasure, we’ll discover the intriguing matter associated to The Energy and Pitfalls of Mathematical Fashions: A Deep Dive. Let’s weave attention-grabbing info and provide recent views to the readers.

The Energy and Pitfalls of Mathematical Fashions: A Deep Dive

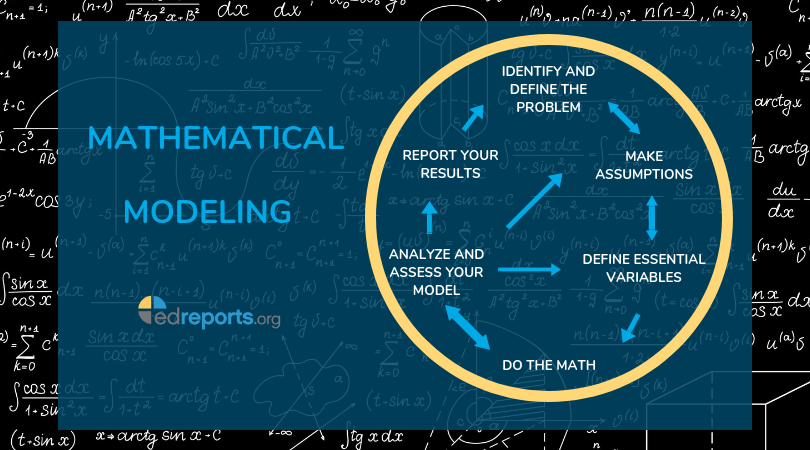
Mathematical fashions are the unsung heroes of recent science, engineering, and even social sciences. They’re summary representations of real-world techniques, processes, or phenomena, expressed utilizing mathematical language. From predicting the climate to optimizing provide chains, from designing airplanes to understanding the unfold of ailments, mathematical fashions present invaluable instruments for evaluation, prediction, and decision-making. Nonetheless, their energy comes with caveats. Understanding each the strengths and limitations of those fashions is essential for his or her efficient and accountable use.

What’s a Mathematical Mannequin?

At its core, a mathematical mannequin is a simplified illustration of actuality. It focuses on key features of a system, ignoring much less necessary particulars to make the issue tractable. This simplification is important as a result of real-world techniques are sometimes extremely complicated, with quite a few interacting variables and unpredictable components. mannequin captures the essence of the system whereas remaining manageable for evaluation.

Fashions can take many types, starting from easy algebraic equations to complicated techniques of differential equations, stochastic processes, and agent-based simulations. The selection of mannequin relies upon closely on the character of the issue, the out there knowledge, and the specified stage of accuracy.

Kinds of Mathematical Fashions:

Mathematical fashions could be categorized in a number of methods:

• Deterministic vs. Stochastic: Deterministic fashions assume that given the identical preliminary situations, the end result will all the time be the identical. They’re ruled by fastened guidelines with no randomness concerned. Examples embody Newtonian mechanics and lots of engineering fashions. Stochastic fashions, then again, incorporate randomness and chance. They’re used when uncertainty is a major issue, equivalent to in monetary modeling, epidemiology, and climate forecasting.

• Static vs. Dynamic: Static fashions symbolize a system at a single cut-off date, offering a snapshot of the system’s state. Dynamic fashions, in distinction, describe how a system adjustments over time. They usually contain differential equations or distinction equations to seize the evolution of the system. Examples embody inhabitants progress fashions and fashions of chemical reactions.

• Discrete vs. Steady: Discrete fashions take care of variables that may solely tackle particular, separate values (e.g., the variety of vehicles on a freeway). Steady fashions, conversely, permit variables to tackle any worth inside a given vary (e.g., the temperature of a room).

• Linear vs. Non-linear: Linear fashions assume a proportional relationship between variables. They’re usually simpler to research however might not precisely symbolize real-world techniques that exhibit complicated interactions. Non-linear fashions seize extra intricate relationships, usually resulting in extra life like however doubtlessly more difficult analyses.

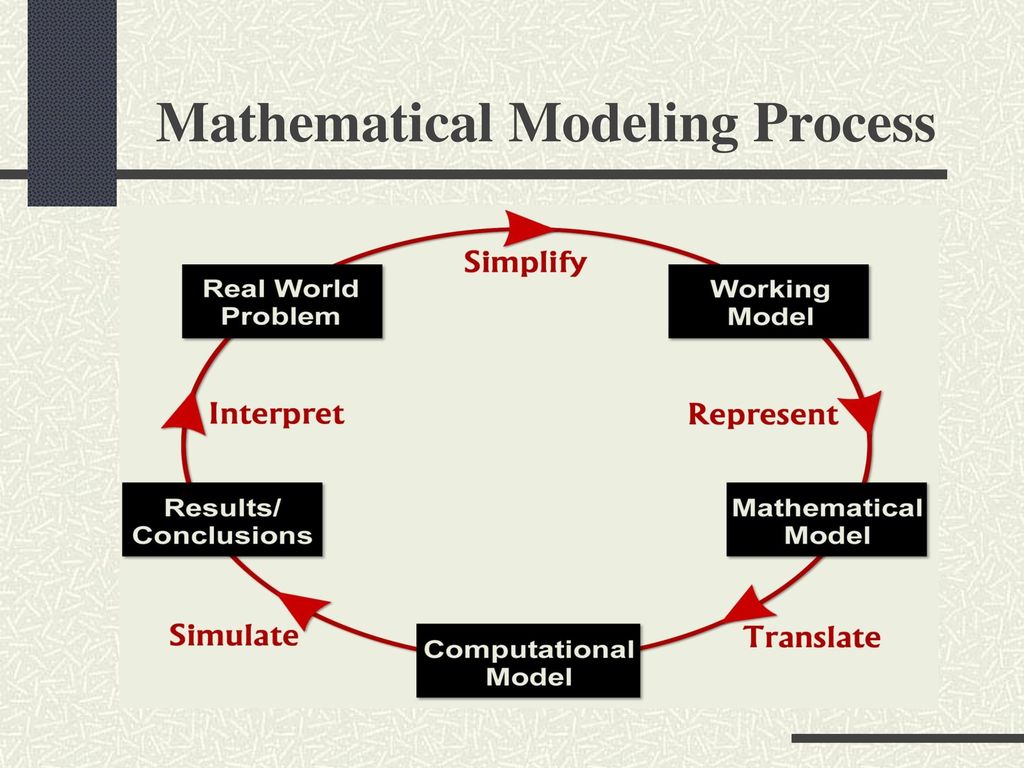
The Modeling Course of:

Constructing a profitable mathematical mannequin is an iterative course of that usually entails the next steps:

1. Downside Definition: Clearly outline the issue you are attempting to unravel and the particular questions you need to reply.

2. Mannequin Formulation: Determine the important thing variables and their relationships. This usually entails making simplifying assumptions and neglecting much less necessary components.

3. Mannequin Improvement: Translate the conceptual mannequin into mathematical equations or algorithms. This may contain selecting acceptable mathematical methods and instruments.

4. Mannequin Validation: Take a look at the mannequin in opposition to real-world knowledge to evaluate its accuracy and reliability. This usually entails evaluating mannequin predictions to noticed outcomes.

5. Mannequin Calibration: Modify the mannequin parameters to enhance its match to the information. That is an iterative course of that entails refining the mannequin primarily based on the validation outcomes.

6. Mannequin Utility: Use the validated mannequin to make predictions, analyze situations, or help decision-making.

Examples of Mathematical Fashions in Totally different Fields:

The functions of mathematical fashions are huge and diverse:

• Physics: Newton’s legal guidelines of movement, Maxwell’s equations of electromagnetism, and Einstein’s idea of relativity are all examples of highly effective mathematical fashions which have revolutionized our understanding of the bodily world.

• Engineering: Mathematical fashions are essential in designing and analyzing buildings, circuits, and techniques. Finite ingredient evaluation, as an illustration, is a broadly used method for simulating the conduct of complicated buildings beneath varied hundreds.

• Economics: Fashions just like the Solow-Swan mannequin are used to research financial progress, whereas the Black-Scholes mannequin is used to cost monetary choices.

• Biology: Compartmental fashions are used to check the unfold of infectious ailments, whereas reaction-diffusion equations are used to mannequin organic sample formation.

• Ecology: Predator-prey fashions and inhabitants dynamics fashions assist us perceive the interactions between species and the components that affect inhabitants sizes.

• Local weather Science: World local weather fashions (GCMs) are complicated techniques of equations that simulate the Earth’s local weather system, offering essential insights into the impacts of local weather change.

Limitations and Pitfalls of Mathematical Fashions:

Regardless of their energy, mathematical fashions have inherent limitations:

• Simplification: The simplification inherent in mannequin constructing can result in inaccuracies and misrepresentations of actuality. Ignoring necessary components can result in flawed predictions and deceptive conclusions.

• Information Limitations: The accuracy of a mannequin relies upon closely on the standard and amount of the out there knowledge. Inadequate or unreliable knowledge can result in unreliable mannequin predictions.

• Mannequin Uncertainty: There may be all the time some extent of uncertainty related to a mathematical mannequin. This uncertainty can stem from the simplifying assumptions, the restrictions of the information, or the inherent randomness within the system being modeled.

• Overfitting: Overfitting happens when a mannequin is just too complicated and suits the out there knowledge too carefully, however fails to generalize effectively to new knowledge. This could result in inaccurate predictions and a false sense of confidence within the mannequin’s accuracy.

• Misinterpretation: Even with a well-validated mannequin, misinterpreting the outcomes can result in flawed conclusions. It is essential to know the mannequin’s assumptions, limitations, and the context through which it’s being utilized.

Conclusion:

Mathematical fashions are highly effective instruments for understanding and predicting the conduct of complicated techniques. They supply useful insights into a variety of phenomena, supporting decision-making in varied fields. Nonetheless, it is essential to acknowledge their limitations and keep away from overreliance on their predictions. A important understanding of the modeling course of, the assumptions made, and the inherent uncertainties is crucial for accountable and efficient use of mathematical fashions. The continuing growth of extra refined fashions, coupled with developments in knowledge science and computing energy, continues to develop the scope and influence of this significant instrument for scientific inquiry and technological development. The way forward for many scientific disciplines hinges on our skill to create, refine, and critically consider more and more complicated and nuanced mathematical fashions.

Closure

Thus, we hope this text has offered useful insights into The Energy and Pitfalls of Mathematical Fashions: A Deep Dive. We recognize your consideration to our article. See you in our subsequent article!